14 Jan 2020

Sanjoy Dasgupta가 저술한 책인 Algorithms과 이기창님의 블로그, Heee님의 블로그를 참고하였다.

1. Heap

1-1. Heap(힙)의 정의

• 완전이진트리의 일종으로, 데이터에서 최대/최소값을 빠르게 찾아내도록 만들어진 자료구조
• 큰 키(우선순위)에 자주 액세스하거나 이를 중심으로 정렬된 시퀀스를 활용할 때 유용
• 중복값을 허용함. cf) Binary Search Tree는 허용하지 않음

쉽게 이해해보자. 만약에 데이터 리스트가 쫘르르~ 있는데, 내가 여기서 가장 큰 값을 찾고 싶으면 일련의 리스트로 구성된 데이터 내에서 힘들게 찾아야 할 것이다. 하지만 만약 데이터가 트리형태로 구성되어 있고, 가장 큰 값이 때마침 루트 노드에 있다면? 당연히 손쉽게 바로 찾을 수 있을 것이다. Heap란 바로 이럴 때 사용하라고 있는 자료구조이다!

cf) Binary Search Tree(BST)

하나의 노드가 최대 두 개의 자식 노드를 갖는 트리. 노드의 값이 반드시 왼쪽 자식노드 $\leq$ 부모노드 $\leq$ 오른쪽 자식노드여야 한다. 참고로 이처럼 트리의 값 구조를 정의하는 방식을 트리순회(Tree Traversal)라고 하며, 완전이진트리는 이중 Inorder방식을 따른다. Heap는 이와 달리 그냥 무조건 부모가 자식보다 크거나 같거나, 작거나 같은 성질을 갖는다.

따라서 BST는 탐색에, Heap은 우선순위 정렬에 주로 사용된다.

Heap의 속성은 다음과 같다.

• Heap Order Property : 각 노드의 값은 자식노드의 값보다 크거나 같고, 혹은 작거나 같다.
• Heap Shape Property : 모양이 완전이진트리이다. 즉, 마지막 레벨의 모든 노드는 왼쪽에 쏠려있다.

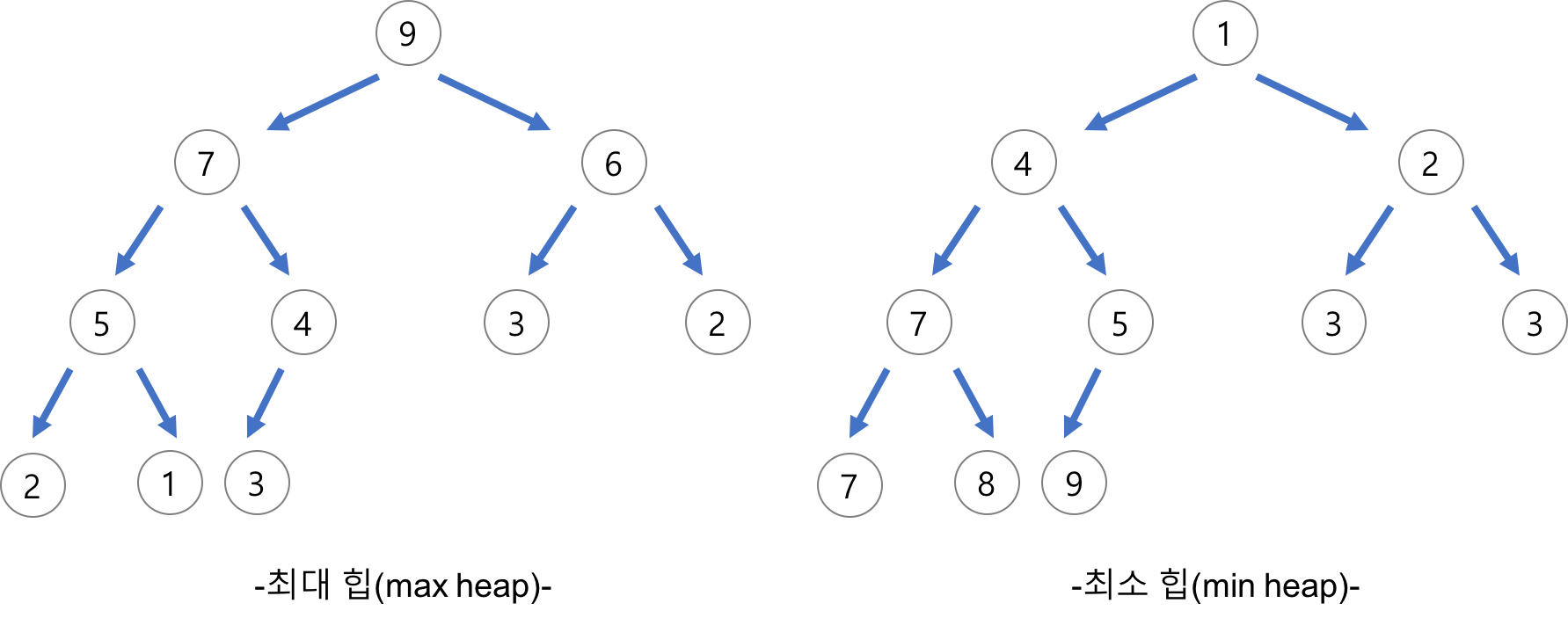
1-2. Heap(힙)의 종류

Heap는 루트노드가 최대값인 Max heap(최대 힙)과 최소값인 Min heap(최소 힙)으로 구성된다. 이들은 모두 recursive한 구조를 갖고 있다.

• Max heap : 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전이진트리

• Min heap : 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전이진트리

  

1-3. Heap(힙)의 구현(Heapify)

일단 Heap의 표준적인 자료구조는 배열(Array)이다.

따라서 완전이진트리 형태의 Heap을 1차원 배열로 나타내면 다음과 같다. 이처럼 완전이진트리를 배열로 나타내면 가장 좋은 점은 인덱스로 바로 접근이 가능하다는 것이다. 따라서 Heap을 구현할 때, 인덱스를 이용해서 바로 바꿔줄 수 있다.

위의 그림을 통해, 어떤 노드의 index의 왼쪽 자식노드와 오른쪽 자식노드의 index를 각각 left_index, right_index라고 한다면 다음과 같은 특성을 알 수 있다.

left_index = index * 2

right_index = index * 2 + 1

이제부터는 구현에 대해 알아보자. 주어진 자료구조를 Heap로 만드는 연산을 Heapify라고 한다. 예를 들어, Max heap을 만드는 Heapify는 다음과 같다.

앞에서 말했듯이, Max heap은 부모노드의 키 값이 자식노드의 키 값보다 반드시 크거나 같아야 한다. 따라서 첫번째 그림의 4의 경우 자식노드중 인덱스가 먼저인 14와 비교했을 때, 4<14이므로 Max heap의 성질을 만족하지 못한다. 따라서 두번째 그림과 같이 바꿔준다.

그러면 두번째 그림에서 볼 수 있듯이 루트 노드인 14는 자식노드 4, 7보다 크므로 Max heap의 성질을 만족하는 것을 알 수 있다. 이어서 내려온 4는 또, 오른쪽 자식노드 8보다 작은 것을 알 수 있다. 따라서 4와 8을 바꿔주면 세번째 그림이 되고, 이는 Max heap의 성질을 모두 만족하는 것을 알 수 있다.

1-4. Heap(힙)의 삽입, 삭제

• Insert(삽입)

  (1) Heap에 새로운 요소는 Heap의 마지막 노드에 삽입된다.(Shape 속성 만족)

  (2) Heap의 성질에 맞게 노드를 교환해준다

  

  이 그림을 보면 새 요소 18이 마지막 노드에 삽입된 뒤, Max heap의 성질을 만족하도록 5와 변경해주고, 다시 16과 변경한 것을 알 수 있다.

• Delete(삭제)

  (1) 루트노드를 삭제한다(Max heap에서의 삭제 연산은 최대값을 삭제하는 것이다)

  (2) 삭제된 루트노드의 자리에 Heap의 마지막 노드를 가져온다.

  (3) Heap의 성질에 맞게 노드를 교환해준다.

  

  이 그림을 보면 루트노드(최대값) 18이 삭제되고, 마지막 노드 5가 루트노드에 가져와진다. 이후 Max heap의 성질을 만족하도록 5를 16과 변경해 준 것을 알 수 있다.

1-5. Heap(힙)의 시간복잡도

• Heapify

  최악의 경우 루트노드에서 잎새노드까지 값을 비교해야 한다. 따라서 트리의 높이 $\log_2n$에 의존적이고, 값을 비교해서 바꾸는 연산은 $O(1)$이므로 시간복잡도는 $O(\log_2n)$이다.

• Heap의 삽입

  삽입하는 데 드는 연산은 $O(1)$이고, 해당 노드를 Heapify하는데 드는 시간은 $O(\log_2n)$이므로 시간복잡도는 $O(\log_2n)$이다.

• Heap의 삭제

  삭제하는 데 드는 연산은 $O(1)$이고, 마지막 노드를 루트노드(삭제 위치)로 옮기는 데 드는 연산은 $O(1)$, 해당 노드를 Heapify하는데 드는 시간은 $O(\log_2n)$이므로 시간복잡도는 $O(\log_2n)$이다.

d진 히프(d-ary Heap)의 경우에는 log의 밑이 2가 아니라 d이다.

2. Heap Sort(힙 정렬)

데이터를 최대 힙 트리나 최소 힙 트리로 구성해 정렬하는 방법.

이제부터는 Max heap을 위주로 설명하려한다. 데이터가 다음과 같이 주어졌다고 하자.

[16, 4, 10, 14, 7, 9, 3, 2, 8, 1]

이를 우선 Insert 방식을 이용해 이진트리로 구성해보면 다음과 같다.

16을 루트노드에 두고 그 다음 4를 왼쪽 자식 노드에, 10을 오른쪽 노드에… 이 과정을 반복한 것이다. 이제 이 트리를 대상으로 heapify를 해보자.

heapify를 할 때 가장 좋은 시작점은 데이터 개수 / 2 의 값을 인덱스로 갖는 노드이다. 이후 이 노드의 자식노드와 값을 비교하며 heapify를 진행한다. 따라서 이 트리의 시작점은 10 / 2 = 5번째 인덱스 노드가 되겠다. 이후 네 번째, 세 번째, 두 번째, 첫 번째 인덱스 노드를 주인공으로 heapify를 진행한다.

• 다섯 번째(7), 네 번째(14), 세 번째(10) : 이미 만족한다.

• 두 번째(4) : 4와 14를 바꿔준다.

  

  이제는 바뀐 4를 보자. 4는 자식노드 2보다 크지만 8보다 작으므로 4와 8을 바꿔줘야 한다.

  

• 첫 번째(16) : 이미 만족한다. 끝!

이처럼 Heap Sort를 하기 위해서는 먼저 값을 Insert 해서 트리를 만든 뒤, 가운데 인덱스에서부터 위로 올라가며 각각의 자식노드와 값을 비교해 heapify를 하면 된다. 어렵지 않다.

3. Heap Sort(힙 정렬)의 특징

• Unstable 하다.

  부모노드와 자식노드를 바꿔가며 정렬하는 과정에서 입력 값의 위치가 바뀔 수 있다.

  예를 들어보자. 루트노드의 값이 5인 트리가 있다.

  루트노드의 왼쪽 서브트리에 하나의 노드가 있다. 이 노드의 값은 6이고 이 노드의 자식노드로 7(1)이 있다.

  그리고 루트노드의 오른쪽 서브트리에 하나의 노드가 있다. 이 노드의 값은 9이고, 이 노드의 자식노드로 7(2)가 있다.

  이때, 이 트리를 Min heap으로 변경하기 위해 heapify를 수행한다고 하자.

  그러면 왼쪽 서브트리는 노드의 값이 5 - 6 - 7(1)이기 때문에 따로 손 댈 필요가 없다.

  그런데 오른쪽 서브트리는 노드의 값이 5 - 9 - 7(2)이기 때문에 9와 7(2)를 바꿔줘야 한다.

  따라서 오른쪽 서브트리는 노드의 값이 5 - 7(2) - 9가 된다.

  이렇게 되면! 트리의 높이 1에 7(2)가 위치하게 되고, 높이 2에 7(1)이 위치하게 되어 같은 값의 위치가 swap된 것을 알 수 있다.

• In-place 하다.

  정렬 수행 과정에서 별도의 저장 공간을 필요로 하지 않는다. 트리 내에서만 움직이기 때문!

4. Heap Sort(힙 정렬)의 장단점

• 장점

  (1) 시간복잡도가 좋은 편이다.

  (2) 가장 큰 값, 작은 값 몇개만 필요할 때 유용하다.

• 단점

  (1) 높이가 $\log_2n$이므로 삽입, 삭제할 때 모두 $\log_2n$ 시간이 소요된다. 이게 단점인가?

5. Heap Sort(힙 정렬)의 시간복잡도

• Best, Average, Worst Case

  힙 트리가 거의 완전이진트리이므로 높이가 $\log_2n$임

  따라서 요소를 Heap에 삽입, 삭제할 때 시간이 $\log_2n$만큼 소요됨.

  이 과정을 거치는 요소가 총 $n$개 이므로 시간복잡도는 Best, Average, Worst Case 모두 $O(n\log_2n)$이다.