Sanjoy Dasgupta가 저술한 책인 Algorithms과 이기창님의 블로그, Heee님의 블로그를 참고하였다.

1. Quick Sort(퀵 정렬)

리스트의 pivot을 선택한 뒤, pivot보다 작은 값과 큰 값으로 리스트를 둘로 분할하는 과정을 반복해 정렬하는 방법

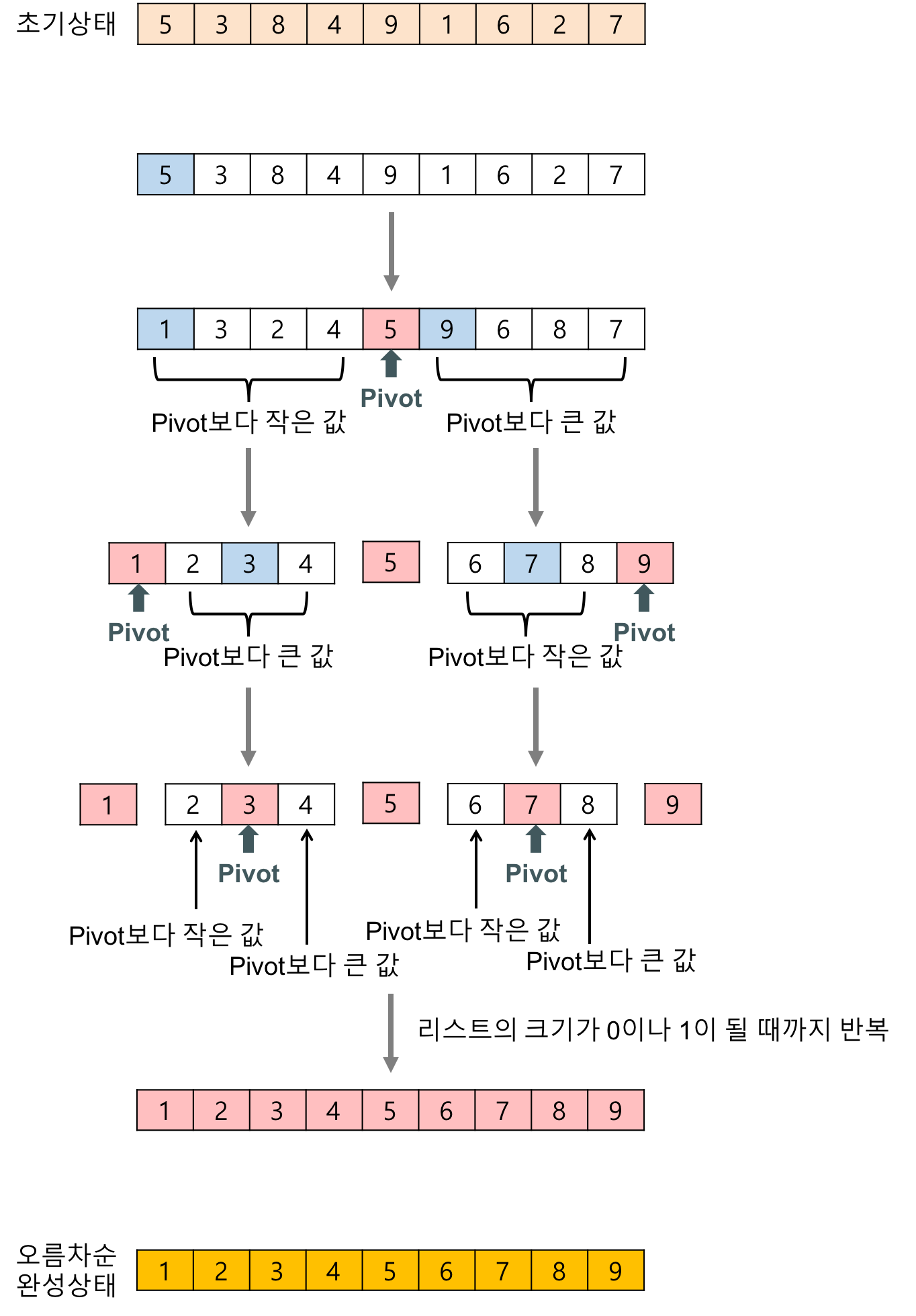
Quick Sort(퀵 정렬)를 그림으로 쉽게 나타내면 다음과 같다.(그림출처)

퀵 소트도 머지 소트처럼 분할(Divide) - 정복(Conquer) - 결합(Combine)의 순으로 정렬이 이루어진다.

1. 리스트에서 하나의 요소(pivot. 피벗)를 선택한다.

2. pivot보다 작은 값을 pivot 앞으로, pivot보다 큰 값을 pivot 앞으로 오도록 하여 리스트를 둘로 분할한다.

3. 분할된 리스트를 기준으로 1~2를 반복한다.(순환 호출)

4. 그럼 최종적으로 이쁘게 정렬된 하나의 데이터가 완성된다.

2. Quick Sort(퀵 정렬)의 특징

• Unstable 하다.

  같은 값을 가진 원소들이 정렬 과정에서 위치(=index)가 뒤바뀔 수 있다.

  다음의 리스트로 예를 들어보자. 리스트의 값과 인덱스는 다음과 같다.

  3(1), 　5(1), 　5(2), 　1(1), 　3(2), 　2(1), 　2(2), 　5(3)

  이때, pivot을 3(1)으로 선택하고 퀵 소트를 진행하면 첫 번째 결과는 다음과 같다.

  1(1), 　2(2), 　2(1), 　3(1), 　3(2), 　5(2), 　5(1), 　5(3)

  따라서 이처럼 같은 값의 상대적 위치가 바뀔 수 있는 것을 알 수 있다.

• In-Place 하다.

  정렬 수행 과정에서 별도의 저장 공간을 필요로 하지 않는다. 머지 소트의 경우 리스트가 쪼개져서 2개, 4개, 8개…로 그 개수가 늘어나지만, 퀵 소트는 피벗을 기준으로 값의 순서만 바꿔주기 때문에 리스트 개수는 1개로 일정하기 때문이다.

3. Quick Sort(퀵 정렬)의 장단점

• 장점

  (1) 속도가 빠르다

  퀵 소트는 아래에서 설명하겠지만 시간복잡도가 $O(n\log_2n)$인데, 같은 시간복잡도를 갖는 정렬보다도 더 빠르다. 이름값을 잘함!

  (2) In-place하기 때문에 추가적인 메모리 공간이 필요하지 않다

• 단점

  피벗값을 어떻게 선택하느냐에 따라 불균형 분할에 의해 수행시간이 더 오래 걸릴 수 있다.이는 매우 치명적인 단점이다… 아래에서 살펴보도록 하자

4. Quick Sort(퀵 정렬)의 시간복잡도

• Best, Worst Case

  

  최선의 경우는 이처럼 피벗을 기준으로 리스트의 원소가 균형적으로 나뉘는 경우이다.

  이렇게 되면 머지소트와 똑같이 높이가 $\log_2n$이고, 각 층에서 $n$개의 요소에 대해 정렬을 수행하기 때문에, 시간복잡도가 $O(n\log_2n)$이다.

• Worst Case

  

  최악의 경우는 이처럼 피벗보다 작은 수, 혹은 큰 수가 매번 하나인 경우이다.

  이렇게 되면 높이가 $n$이 되고, 각 층에서 $n$개의 요소에 대해 정렬을 수행하기 때문에 시간복잡도가 $O(n^2)$이 되버린다. 완전 최악!