Sanjoy Dasgupta가 저술한 책인 Algorithms과 이기창님의 블로그, Heee님의 블로그를 참고하였다.

1. Merge Sort(합병정렬)

데이터를 쪼갤 수 없을 때 까지 쪼갠 뒤(Devide), 둘씩 크기를 비교해 정렬하며(Conquer) 합치는(Merge) 방법

Merge Sort(합병정렬)를 그림으로 쉽게 나타내면 다음과 같다.(그림출처)

1. 기존에 $p$(시작점)부터 $r$(끝점)까지 데이터가 있었다면 , $q$(기준점)를 기준으로 데이터를 두 개로 쪼갠다.
2. 다시 쪼개진 각각의 데이터의 $p$와 $r$로부터 $q$를 선정하여 쪼개며, 데이터가 더이상 쪼개질 수 없는 최소의 단위가 될 때 까지 이를 반복한다.
3. 쪼개진 데이터를 두 개씩 비교하며 정렬하며 합친다.
4. 다시 합쳐진 데이터를 또 두 개씩 비교해서 정렬하며 합치며, 모든 데이터가 하나로 합쳐질 때 까지 이를 반복한다.
5. 그럼 최종적으로, 이쁘게 정렬된 하나의 데이터가 완성된다.

2. Merge Sort(합병정렬)의 특징

우선 정렬 알고리즘은 Stable 한지, 그리고 In-place 한지에 따라 성격이 구분된다.

- Stable : 같은 값의 위치(순서)가 정렬 과정에서 뒤바뀌지 않는 경우

- In-place : 탐색대상을 정렬할 때 추가적인 메모리 공간이 필요하지 않은 경우(데이터가 저장된 그 공간에서 정렬이 가능)

그렇다면 Merge Sort는 어떨까?

• Stable 하다.

  Merge Sort는 Devide하는 단계에서 각 node의 index가 변하지 않고, Merge 하는 과정에서도 같은 key 값을 가지는 node가 swap되지 않기 때문에 index가 변하지 않는다. 따라서 Stable 하다.

• In-place할 수도 있고 아닐 수도 있다.

  연결리스트와 배열 중 자료구조로 무엇을 쓰느냐에 따라 In-place할 수도 있고 아닐 수도 있다.

  
  

  (1) 연결리스트(Linked list) : 각 노드가 데이터와 포인터를 갖고 한 줄로 연결되어 있는 방식으로 데이터를 저장하는 자료구조

  

  연결리스트를 사용하게 되면 기존 저장공간에서 포인터만 바꾸는 형식으로 머지소트를 수행할 수 있다. 따라서 따로 리스트를 저장할 별도의 공간이 필요하지 않기 때문에 In-place 하다.

  
  

  (2) 배열(Array) : 같은 종류의 데이터들이 순차적으로 저장된 자료구조

  

  배열은 리스트를 쪼갤 경우 쪼개진 리스트를 별도로 저장할 공간이 없기 때문에 In-place하지 않다.

  
  

  따라서 머지소트의 경우 연결리스트와 배열 중 어떤 자료구조를 사용하느냐에 따라 In-place 할 수도 있고 아닐 수도 있다. (이후에 공부할 Quick Sort와 Heap Sort는 모두 Unstable하고 In-Place하다!)

3. Merge Sort(합병정렬)의 장단점

• 장점

  (1) Stable 하기 때문에 안정적이다. 따라서 데이터 분포에 영향을 덜 받으므로 어떤 데이터가 입력되어도 정렬 시간$(O(n\log_2n))$은 동일하다.

  (2) 자료구조로 연결리스트를 사용한다면 링크 인덱스만 변경되므로 데이터의 이동이 무시할 수 있을 정도로 작아진다. 즉, In-Place 하다. 따라서 크기가 큰 레코드를 정렬할 경우 자료구조로 연결리스트를 사용한다면 정렬 방법 중 가장 효율적이다.

• 단점

  자료구조로 배열을 사용한다면 쪼개진 데이터를 별도로 저장할 공간이 필요하기 때문에 In-Place하지 못하다. 이 경우, 크기가 큰 레코드를 정렬한다면 매우 큰 시간적 낭비를 초래한다.

4. Merge Sort(합병정렬)의 시간복잡도

• Best, Average, Worst Case

  

  • $n$이 2의 거듭제곱이라고 가정할 때, 기존의 $n$개의 데이터를 각각 $n/2$개인 데이터 2개로 쪼개고, 또 $n/2$개인 데이터를 각각 쪼개서 각각 $n/4$개인 데이터 4개를 만들고………..이 과정이 반복된다.

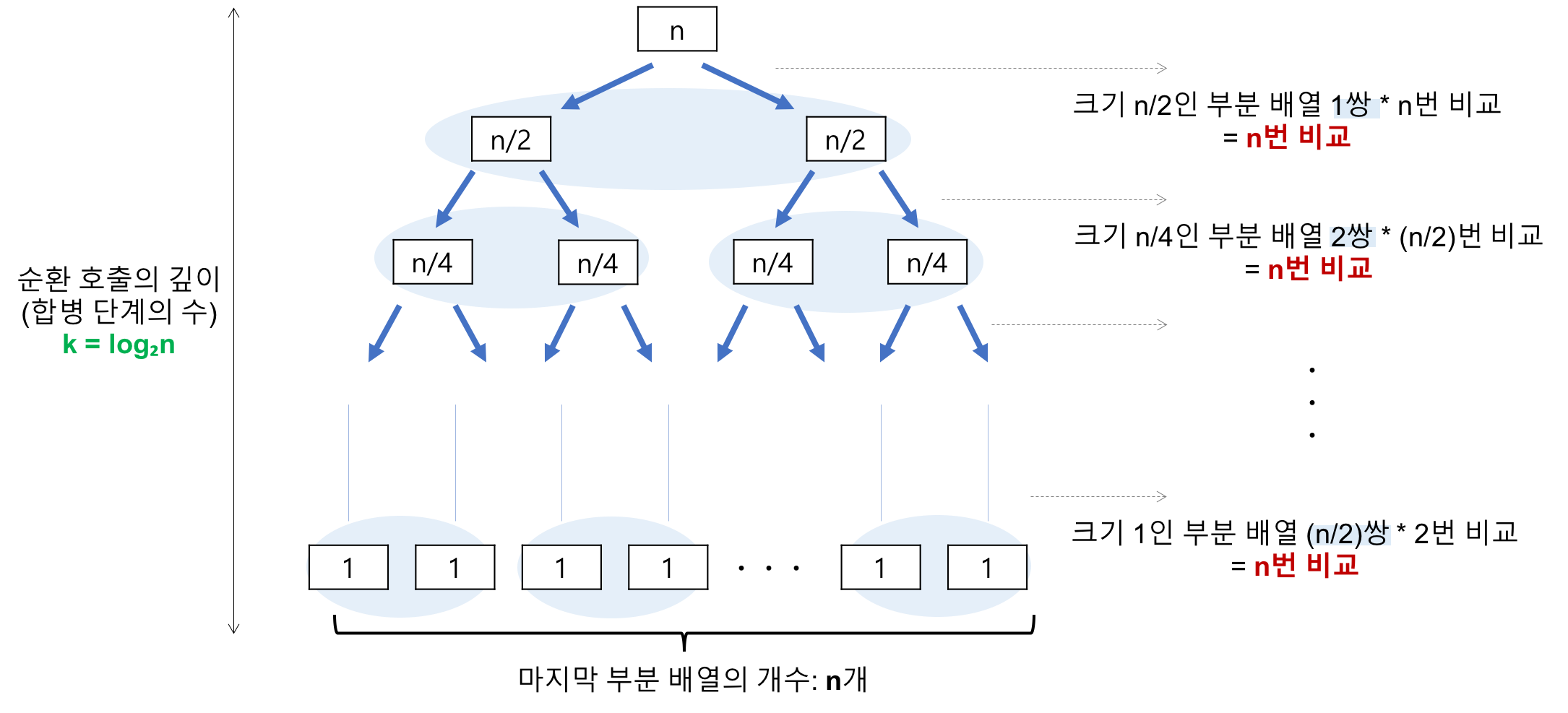
  • 이때, 가장 처음! $n$개일 때의 데이터의 높이를 0이라고 하면, $n/2$개일 때는 1, $n/4$개일 때는 2로 내려갈 때마다 높이가 1 씩 증가하는데, 이 높이는 $k = \log_2n$과 같다.

  • 그리고 높이가 0일 때는 $n$번 비교, 높이가 1일 때는 $n/2 * 2 = n$번 비교…………..인 것처럼, 매 높이마다 항상! 똑같이! $n$번 비교하는 것을 알 수 있다.

    
    

    따라서! 머지소트를 수행하는 동안 데이터로부터 만들어진 높이($\log_2n$)안에서, 각 높이별로 $n$번 비교하고 정렬하기 때문에 Merge Sort의 시간복잡도는 Best, Average, Worst Case 모두 $O(\log_2n) * O(n)$ = $O(n\log_2n)$임을 알 수 있다.

참고로 시간복잡도를 매스터 정리로 구하는 방법은 다음과 같다.

1. $ T(n) = 2T(\frac n 2) + O(n)$
2. $a = 2, b = 2, d = 1$ 이므로
3. 시간복잡도는 $O(n\log_2n)$