Sanjoy Dasgupta가 저술한 책인 Algorithms를 참고하였다.

1. Divide and Conquer Algorithm(분할정복 알고리즘)

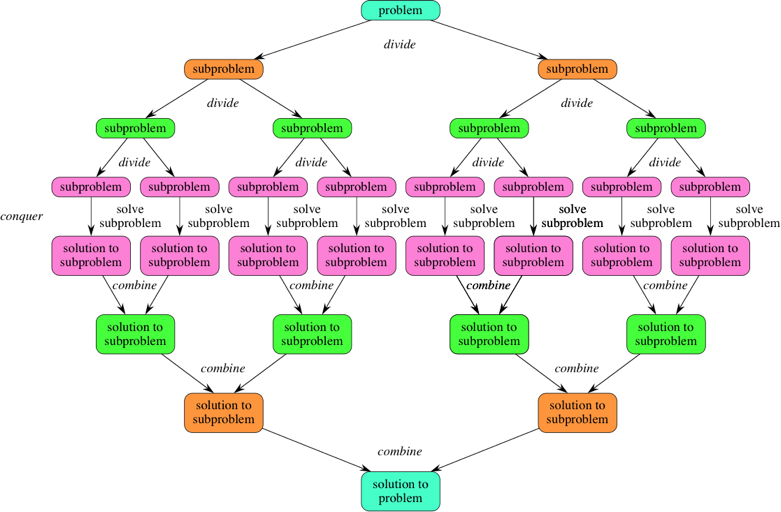
문제를 나눌 수 없을 때 까지 나눈 뒤, 각각을 풀면서 다시 합쳐 문제의 답을 얻는 알고리즘. 전체를 대상으로 하는 것보다 전체를 이루는 부분을 위주로 문제를 해결하고 이들의 결과를 합치는 것이 시간복잡도 측면에서 더 효율적이기 때문에 사용된다.

2. Master theorem(매스터 정리)

분할정복 알고리즘은 종종 일반적인 패턴을 따르는데, 그것은 다음과 같다.

크기 $n$의 문제에 $O(n^d)$ 시간으로, 각각 $\frac n b$인 $a$개의 부문제로 나눈 뒤 재귀적으로 풀며 다시 결합

따라서, 분할정복 알고리즘의 소요 시간은 $T(n) = aT(\frac n b) + O(n^d)$으로 나타낼 수 있으며, $a$, $b$, $d$의 관계를 이용하여 조건별로 시간복잡도를 구하면 다음과 같다.

1. $d$ > $\log_ba$ 　: 　$T(n) = O(n^d)$
2. $d$ = $\log_ba$ 　: 　$T(n) = O(n^d\log n)$
3. $d$ < $\log_ba$ 　: 　$T(n) = O(n^{log_ba})$

예를들어, 곱셈의 경우 실행시간이 $T(n) = 3T(\frac n 2) + O(n)$이다.

$a$ = 3, $b$ = 2, $d$ = 1이므로 매스터 정리의 (3)에 해당된다. 따라서 시간복잡도는 $O(n^{log_23})$이다.

3. 중앙값 구하기

리스트 $S$가 있고 정수 $k$가 있을 때, $S$에서 $k$번째로 작은 원소를 찾는다고 하자.

이때, 무작정 전체 리스트 $S$에서 $k$번째로 작은 원소를 찾는것 보다는, 리스트 $S$에서 임의의 정수 $v$를 선정하여 리스트를 분할(Devide)하고, 각각의 리스트에서 $k$번째로 작은 “그 원소”를 찾은 뒤 다시 합치는(Conquer)방식이 더 효율적일 것이다.

$v$를 선정한다면 리스트 $S$를 각각 $S_L$($v$보다 작은 원소들), $S_v$($v$와 같은 원소들), $S_R$($v$보다 큰 원소들)로 나눌 수 있다.

이렇게 되면 정수 $k$의 값에 따라 $S$의 선택 방법을 다음과 같이 구분할 수 있다.절댓값 기호는 리스트의 원소 개수를 의미한다.

1. $k$ $\leq$ $\left\vert S_L \right\vert$　: 　Selection($S$, $k$) = Selection($S_L, k$)

2. $\vert S_L \vert$ $\leq$ $k$ $\leq$ $\vert S_L \vert + \vert S_v \vert$ 　: 　Selection($S$, $k$) = $v$

3. $k$ $\geq$ $\left\vert S_L \right\vert + \vert S_v \vert$ 　: 　Selection($S$, $k$) = Selection($S_R, k-\vert S_L \vert - \left\vert S_v \right\vert$)

이해를 위해 예를 들어보자.

$S$ : 2, 36, 3, 21, 8, 13, 11, 20, 5, 4, 1, 　$v$ = 7

$S_L$ : 2, 3, 4, 1
$S_V$ : 7
$S_R$ : 36, 21, 8, 13, 11, 20

1의 경우, 내가 2번째로 작은 원소(2)를 찾고 싶은데,
이때, $S_L$의 개수가 3개이므로 $S_L$에서만 찾으면 됨을 알 수 있다. = $(S_L, 2)$

2의 경우, 내가 5번째로 작은 원소(7)를 찾고 싶은데,
이때, 5가 $S_L$의 원소의 개수보다는 크거나 같고, $S_L$과 $S_R$의 원소의 개수의 합보다는 작거나 같으므로 count가 정확히 5이다. 따라서 $S_v$에서만 찾으면 됨을 알 수 있다. = 5

3의 경우 내가 8번째로 작은 원소(13)를 찾고 싶은데,
이때, 8이 $S_L$과 $S_v$의 원소의 개수의 합보다 크므로 $S_R$에서만 찾으면 됨을 알 수 있다. = $(S_R, 3)$

따라서 이처럼 분할정복 방법을 이용하면 값을 찾는 횟수를 최악의 경우였던 $\vert S \vert$에서 $\max(\vert S_L \vert, \vert S_R \vert)$까지 줄일 수 있다.

일반적으로 $v$가 $\frac 1 4$ ~ $\frac 3 4$ 백분위 수 안에 놓이면, 그 값을 찾기에 시간적 측면에서 효율적이라고 평가하고 있다.

이때, 중앙값은 보통 이 백분위 수 안에 있기 때문에, 중앙값을 찾는 시간은 다음과 같이 구할 수 있다.

크기 n의 배열에 취해진 시간 $\leq$ (배열을 $\frac 3 4n$크기 이하로 줄이는 시간 + $\frac 3 4n$ 크기의 배열에 취해진 시간)

따라서 $T(n) \leq T(\frac 3 4n) + O(n)$이므로 매스터 정리를 이용하면 시간복잡도가 $O(n)$임을 알 수 있다.